1. n 노드에 있는 트리의 가장 작은 높이는 Ω(lgn) = -1 + lg(n+1)임을 증명하십시오.
트리에 n개의 노드가 있고 d의 깊이가 있다고 가정합니다.
루트 노드는 1개의 노드를 가지며 깊이가 1이면 최대 2개의 노드가 생성됩니다. 깊이가 2이면 최대 2^2 = 4개의 노드가 생성됩니다. 그리고 깊이가 d이면 최대 2^d개의 노드가 생성됩니다.
n < = 1 + 2 + 2^2 + ⋯ + 2^d와 같은 부등식을 얻을 수 있습니다.
이것은 수학적 귀납법으로 n <= 2^(d+1) -1로 표현할 수 있습니다.
위 식을 풀 때 가장 작은 높이를 찾아야 하므로,
n+1 <= 2^(d+1)
lg2(n+1) <= d+1
lg2(n+1) -1 <= 디.
따라서 n개의 노드가 있는 트리에서 가장 작은 높이 d는 lg2(n+1) – 1과 같으며 이는 Ω(lgn)으로 표현될 수 있습니다.
따라서 Ω(lgn) = lg2(n+1) – 1입니다.
2. 임의 액세스 배열의 공간을 줄이는 경우 연결 목록 데이터 구조를 사용할 수 있습니다. 연결 리스트를 사용한다면 어떤 문제가 생길까요? 시간 복잡도를 설명하여 답을 보여주십시오.
연결 리스트는 연속된 공간 없이 데이터를 저장할 수 있고 미리 공간을 백업할 필요가 없다는 장점이 있다. 그러나 링크 필드를 위한 추가 공간이 필요하고 순차 검색을 하기 때문에 검색 속도가 떨어지는 단점이 있다. 따라서 요소에 액세스하는 시간 복잡도가 연결된 목록에 직접 액세스하는 배열보다 더 나쁘다는 것을 알 수 있습니다.
직접 액세스 배열은 간단한 포인터 산술을 사용하여 요소에 직접 액세스할 수 있으므로 주어진 인덱스에서 요소에 액세스하는 데 O(1) 시간이 걸립니다. 연결된 목록은 원하는 요소에 액세스하기 위해 루트에서 n에 액세스해야 하기 때문에 O(n) 시간이 걸립니다.
따라서 직접 액세스 배열 대신 연결 목록을 사용하면 액세스하려는 요소에 도달하는 데 시간이 더 오래 걸립니다.
4. 생일 기록을 활용하세요. 다음과 같이 진행하십시오.
4.1 순서가 지정되지 않은 배열에 세트로 삽입

4.2 정렬된 배열 집합에 삽입
4.3 직접 액세스 어레이 세트에 넣기

랜덤액세스 어레이 셋을 만드는 방법을 몰라서 chatGPT에서 도움을 받았습니다….
4.5 크기 비교
사이즈는 모두 동일합니다(97(생일수)).
4.6 인터페이스 비교: build, find, insert, delete, find_min, find_max, find_next, find_prev
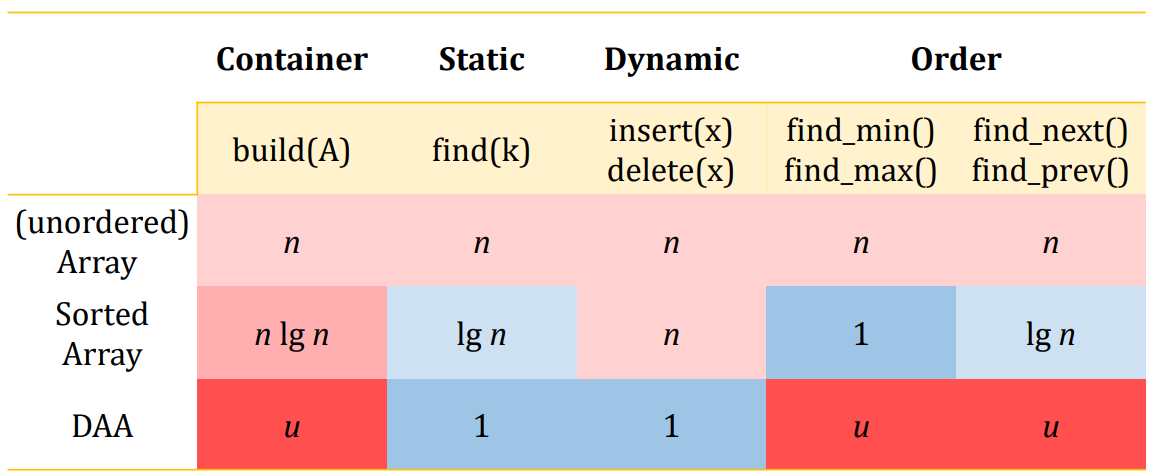
위 사진과 비교해보세요.
| 짓다 | 찾다 | 삽입 | 끄다 | find_min | find_max | 다음 찾기 | find_prev | |
| 정렬되지 않은 배열 | 97 | 97 | 97 | 97 | 97 | 97 | 97 | 97 |
| 정렬된 배열 | 97lg97 | LG97 | 97 | 97 | 하나 | 하나 | LG97 | LG97 |
| 랜덤 액세스 배열 | 97 | 하나 | 하나 | 하나 | 97 | 97 | 97 | 97 |
랜덤 액세스 배열의 범위는 (i,…u-1)이므로 u = n이므로 결과는 위의 표와 유사합니다.
