이것은 DFS 및 BFS 솔루션 모두에서 알려진 검색 문제입니다.
백준 – 2667: 넘버링만
https://www.acmicpc.net/problem/2667
2667: 복소수 넘버링
에서와 같이
www.acmicpc.net
이 문제를 간단히 소개합니다. 정사각형 카드가 있는 경우 1은 집을 의미하고 0은 집이 없음을 의미합니다. 이 지도로 집들이 연결된 단지를 정의하고 단지에 번호를 매겨야 합니다. 여기서 같은 단지는 집의 좌우, 위, 아래에 다른 집들이 있는 경우를 말한다. 그러나 대각선에 집이 있으면 인접한 집이 아닙니다.
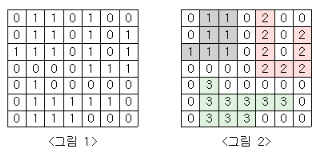
입력으로 첫 번째 행에는 맵의 크기 N(정사각형이므로 너비와 높이가 동일, 5 ≤ N ≤ 25)이 입력되고 다음 N 행에는 모든 N 행렬 유형(0 또는 1)이 입력됩니다. 맵의 최대 크기는 10000을 넘지 않기 때문에 시간복잡도는 크게 고려하지 않아도 된다.
출력은 첫 번째 줄에 있습니다. 전체 단지수를 출력할 수 있으며, 각 단지의 세대수를 오름차순으로 정렬하여 한 줄에 하나씩 출력할 수 있습니다.
예)
입출력
7 3
0110하나00 7
0110하나0하나 8일
1110하나0하나 9
0000111
0하나00000
0111110
0111000
접근1. FSO
주요 기능의 중요한 부분
이 코드의 BFS 함수는 특정 컴플렉스 검색이 완료되면 BFS 코드를 종료합니다. 이 경우 주 기능에서 하나의 유리만 검사하므로, 리본와 함께 “아직 방문하지 않았으며 집이 존재합니다.찾고자 하는 집의 위치를 검색하여 BFS로 다시 진행해야 합니다. 집의 수를 세십시오. 당신이 준 변수를 초기화하십시오.
BFS 기능의 중요한 부분
BFS로 문제를 풀 때 가장 중요한 설정은 대기줄이 문제에서 집의 위치는 2차원 행렬의 형태로 대기합니다. . 쌍문제를 해결하기 위해 대기열에 저장합니다.
이 시점에서 대기열이 빌 때까지 대기열에 저장된 모든 집을 방문하십시오.해야 위, 아래, 왼쪽 및 오른쪽 탐색집의 수를 센다
코너 드롭 배열)
1. 메인 함수에서 리본을 통해 아직 방문하지 않은 모든 기존 주택의 위치 탐색해야한다.
2. BFS 기능에서 queue는 방문할 집의 위치를 저장하기 위해 pair vector 형태로 사용되어야 합니다. 대기열에 저장된 집의 위치는 존재하지만 아직 방문하지 않은 집자아 좌표 검증거쳐간 집입니다(또한 상하좌우 검색시 기존집의 두 좌표에 좌표이동배열을 추가하여 해결합니다.)
int dx() = { 1, 0, -1, 0 } // 첫 번째 좌표 이동 배열
int dy() = { 0, 1, 0, -1 } // 두 번째 좌표 이동 배열
cnt = 단지 내 존재하는 집의 수 세기
n = 지도 크기 선언
vector <vector<int>> map // 지도 벡터
vector <vector<int>> visited // 방문 여부 확인 벡터
vector <int> output // 단지 내 존재하는 집의 수 저장 벡터
int main(){
cin >> n
map.resize(n, vector<int>(n, 0))
visited.resize(n, vector<int>(n, 0))
cnt = 0
for (i = 0; i < n; i++) {
string s
cin >> s
for (j = 0; j < n; j++) {
map(i)(j) = s(j) - '0'
}
}
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
if ((map(i)(j) == 1) && (visited(i)(j) != 1)) {
BFS(i, j)
output.push_back(cnt)
cnt = 0
}
}
}
sort(output.begin(), output.end());
cout << output.size() << endl
for (i = 0; i < output.size(); i++) {
cout << output(i) << endl
}
}
void BFS(int f, int s) {
queue<pair<int, int>> q
visited(f)(s) = 1
q.push(make_pair(f, s))
cnt += 1
while (!q.empty()) {
int now_x = q.front().first // 집의 행 위치
int now_y = q.front().second // 집의 열 위치
q.pop()
for (i = 0; i < 4; i++) {
int x = now_x + dx(i)
int y = now_y + dy(i)
if ((x >= 0) && (y >= 0) && (x < n) && (y < n)) {
if ((map(x)(y) == 1) && (visited(x)(y) == 0)) {
q.push(make_pair(x, y))
cnt += 1
visited(x)(y) = 1
}
}
}
}
}
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
static int dx() = { 1, 0, -1, 0 };
static int dy() = { 0, 1, 0, -1 };
int cnt;
static int n;
static vector <vector<int>> map;
static vector <vector<int>> visited;
static vector <int> output;
void BFS(int f, int s);
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
map.resize(n, vector<int>(n, 0));
visited.resize(n, vector<int>(n, 0));
cnt = 0;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
for (int j = 0; j < n; j++) {
map(i)(j) = s(j) - '0';
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ((map(i)(j) == 1) && (visited(i)(j) != 1)) {
BFS(i, j);
output.push_back(cnt);
cnt = 0;
}
}
}
sort(output.begin(), output.end());
cout << output.size() << endl;
for (int i = 0; i < output.size(); i++) {
cout << output(i) << endl;
}
}
void BFS(int f, int s) {
queue<pair<int, int>> q;
visited(f)(s) = 1;
q.push(make_pair(f, s));
cnt += 1;
while (!q.empty()) {
int now_x = q.front().first;
int now_y = q.front().second;
q.pop();
for (int i = 0; i < 4; i++) {
int x = now_x + dx(i);
int y = now_y + dy(i);
if ((x >= 0) && (y >= 0) && (x < n) && (y < n)) {
if ((map(x)(y) == 1) && (visited(x)(y) == 0)) {
q.push(make_pair(x, y));
cnt += 1;
visited(x)(y) = 1;
}
}
}
}
}
접근2. DFS
주요 기능의 중요한 부분
DFS 기능의 실행은 BFS와 마찬가지로 특정 콤플렉스를 모두 검색하면 종료됩니다. 따라서 BFS와 같은 주요 기능에서 리본와 함께 “아직 방문하지 않았으며 집이 존재합니다.“집의 위치를 찾습니다. 여기서 BFS와 다른 점은 DFS 함수가 재귀 함수이므로 처음 방문한 집을 함수 내에서 계산하지 않는다는 것입니다. 카운트의 시작0이 아닌 값으로 하나from (함수 안에서 세면 집 수를 두 배로 한 결과를 얻습니다.)
DFS 기능의 중요한 부분
DFS 함수는 별도의 큐를 사용할 필요 없이 위, 아래, 왼쪽, 오른쪽을 반복합니다. 좌표 확인 통과하다 아직 방문하지 않고 존재하는 집반대편 재귀 함수계속 찾아야 합니다.
코너 가을 배열)
1. 메인 함수에서 리본을 통해 아직 방문하지 않은 모든 기존 주택의 위치 탐색해야한다. 그리고 집의 수는 첫 번째 집을 포함하여 1부터 세게 됩니다.
2. DFS 기능에서 queue를 사용하지 않고 조건이 만족되면, 재귀검색을 계속하십시오
int dx() = { 1, 0, -1, 0 } // 첫 번째 좌표 이동 배열
int dy() = { 0, 1, 0, -1 } // 두 번째 좌표 이동 배열
cnt = 단지 내 존재하는 집의 수 세기
n = 지도 크기 선언
vector <vector<int>> map // 지도 벡터
vector <vector<int>> visited // 방문 여부 확인 벡터
vector <int> output // 단지 내 존재하는 집의 수 저장 벡터
int main(){
cin >> n
map.resize(n, vector<int>(n, 0))
visited.resize(n, vector<int>(n, 0))
cnt = 0
for (i = 0; i < n; i++) {
string s
cin >> s
for (j = 0; j < n; j++) {
map(i)(j) = s(j) - '0'
}
}
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
if ((map(i)(j) == 1) && (visited(i)(j) != 1)) {
DFS(i, j)
output.push_back(cnt)
cnt = 1 // 첫 번째 방문한 집을 포함하여 1부터 세기
}
}
}
sort(output.begin(), output.end());
cout << output.size() << endl
for (i = 0; i < output.size(); i++) {
cout << output(i) << endl
}
}
void DFS(int f, int s) {
visited(f)(s) = 1
for (i = 0; i < 4; i++) {
int x = f + dx(i) // 집의 행 위치
int y = s + dy(i) // 집의 열 위치
if ((x >= 0) && (y >= 0) && (x < n) && (y < n)) {
if ((map(x)(y) == 1) && (visited(x)(y) == 0)) {
cnt += 1
visited(x)(y) = 1
DFS(x, y) // 재귀 탐색
}
}
}
}
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
static int dx() = { 1, 0, -1, 0 };
static int dy() = { 0, 1, 0, -1 };
int cnt;
static int n;
static vector <vector<int>> map;
static vector <vector<int>> visited;
static vector <int> output;
void DFS(int f, int s);
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
map.resize(n, vector<int>(n, 0));
visited.resize(n, vector<int>(n, 0));
cnt = 1;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
for (int j = 0; j < n; j++) {
map(i)(j) = s(j) - '0';
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ((map(i)(j) == 1) && (visited(i)(j) != 1)) {
DFS(i, j);
output.push_back(cnt);
cnt = 1;
}
}
}
sort(output.begin(), output.end());
cout << output.size() << endl;
for (int i = 0; i < output.size(); i++) {
cout << output(i) << endl;
}
}
void DFS(int f, int s) {
visited(f)(s) = 1;
for (int i = 0; i < 4; i++) {
int x = f + dx(i);
int y = s + dy(i);
if ((x >= 0) && (y >= 0) && (x < n) && (y < n)) {
if ((map(x)(y) == 1) && (visited(x)(y) == 0)) {
cnt += 1;
visited(x)(y) = 1;
DFS(x, y);
}
}
}
}